|
|
|
|
|
EJERCICIO
5 |
|
Equilibrio
en el plano - Cálculo de reacciones
|
|
La estructura que
ilustra la figura está cargada con las fuerzas P1 y P2, aplicadas
en su extremo superior. Se desea calcular gráfica y analíticamente
las reacciones de apoyo.
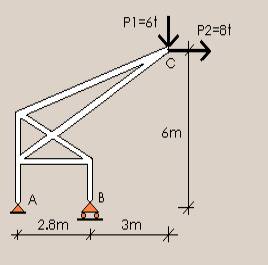
Para calcular el valor de las
reacciones en forma gráfica, el primer paso es determinar la
dirección y el sentido de la resultante de las cargas. Con una
construcción simple se lo logra: dibujamos a escala de fuerzas P1,
a continuación dibujamos (en la misma escala) P2; al unir el
comienzo de P1 con el final de P2 se obtiene la resultante R1 de
ambas. |
|
|
|
|
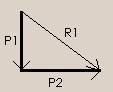
Si
trasladamos la resultante al esquema de cargas R1, aplicándola en el
punto C, reemplazando P1 y P2, tendremos en el plano un sistema de
tres fuerzas, que serán concurrentes. ¿Porqué? Si el sistema está
en equilibrio es porque no tiene desplazamientos en ningún sentido,
ni giros. Y cuando las fuerzas del sistema son concurrentes no hay
manera de que se genere un brazo de palanca entre dos o más de esas
fuerzas. |
|
|
|
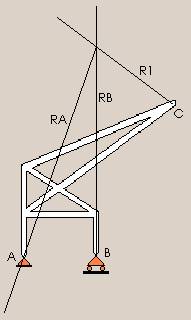
| La
dirección de la reacción que genera el apoyo B es conocida
por las características del vínculo: desplazable, o sea que
la reacción posible es solamente perpendicular al plano de
apoyo. Por lo tanto tendremos un sistema de tres fuerzas
concurrentes de las cuales conocemos las direcciones de dos de
ellas. Averiguar la tercera el cuestión de dibujarlo.
Conociendo las direcciones de
las tres, y el sentido de una, se puede dibujar el polígono
cerrado para determinar cada sentido y, a escala de fuerzas,
el módulo o magnitud.
Únicamente
se necesita medir a escala cada segmento para conocer su valor.
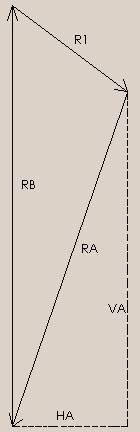
Se
hace notar que la componente VA de RA va hacia abajo mientras
que la componente HA va hacia la izquierda. |
|
|
|
|
|
|
Pasemos
ahora a la resolución analítica. Como es un problema de equilibrio en el
plano, lo primero que hacemos es presentar las tres ecuaciones de la estática |
|
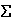 Fx
= 0 Fx
= 0
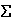 Fy
= 0 Fy
= 0
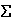 M
= 0 M
= 0
|
|
Comencemos
con una ecuación de momento, y para ello elijaimos como centro de giro el
punto A. |
|
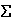 MA
= 0 = P1 x d1 + P2 x d2 + RB dAB = 0
reemplazamos, ahora teniendo en cuenta el sentido de giro MA
= 0 = P1 x d1 + P2 x d2 + RB dAB = 0
reemplazamos, ahora teniendo en cuenta el sentido de giro
|
|
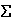 MA
= 0 = (+6t x 5.80m) + (+8t x 6m) + (-RB x 2.80m) = 0 despejamos el término que contiene la incógnita MA
= 0 = (+6t x 5.80m) + (+8t x 6m) + (-RB x 2.80m) = 0 despejamos el término que contiene la incógnita
|
|
RB
x 2.80m = +34.80 tm + 48 tm = 82.80 tm
despejando RB |
|
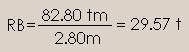
|
|
Para
conocer el valor de la componente VA planteamos la ecuación de
proyecciones sobre un eje paralelo a las y |
|
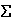 Fy
= 0 = P1 + RB + VA = 0
no se han tenido en cuenta los sentidos de estas fuerzas; ahora
reemplazando Fy
= 0 = P1 + RB + VA = 0
no se han tenido en cuenta los sentidos de estas fuerzas; ahora
reemplazando
|
|
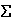 Fy
= 0 = -6t + 29.57t – VA = 0
de aquí despejamos VA VA
= 23.57t Fy
= 0 = -6t + 29.57t – VA = 0
de aquí despejamos VA VA
= 23.57t
|
|
y va hacia abajo ya que en la ecuación anterior hemos puesto el
signo negativo |
|
Para
determinar el valor de la componente HA es suficiente con plantear la
ecuación de proyecciones de fuerzas sobre un eje paralelo a las x |
|
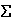 Fx
= 0 = +P2 + HA = 0
reemplazando Fx
= 0 = +P2 + HA = 0
reemplazando
|
|
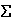 Fx
= 0 = 8t –HA = 0
de donde HA
= 8t Fx
= 0 = 8t –HA = 0
de donde HA
= 8t
|
| {{{{{ }}}}} |
|

|
Este ejercicio ha sido
presentado y desarrollado en la publicación ESTRUCTURAS EN
ARQUITECTURA - Primer Nivel cuyo autor es el Ingeniero José
Luis Gómez |
|
|
|